高校数学IIIの教科書における積分の計算問題の背景
#数楽 手元にある高校数学IIIの教科書のデータを見ると確かに積分計算の問題がつまらなく見えるな。高木貞治『解析概論』に載っている計算例であれば面白く見える。計算例が面白くないのは非常にまずい。『解析概論』の配布が必要か?https://twitter.com/sekibunnteisuu/status/848024346907951104 …
#数楽 もう一歩進めば面白い話になる計算を途中でやめたり、どのように一般化されるかにまったく触れなかったりで、高校数学IIIの教科書だけを見て積分計算の面白さを十分に理解することは不可能だと思う。先生の側が高木貞治『解析概論』程度の一般教養を身に付けていれば大丈夫だと思いますが。
#数楽 学生時代にはつまらない計算例だと思っていた高木貞治『解析概論』p.113の例3が結構面白い計算例だったことに今頃になって気付いたりしている。『解析概論』を読んでいた時期にはポリログなんて知らなかったからなあ。https://twitter.com/i/moments/845090941903892480 …
@sekibunnteisuu 数3の積分でも物理現象や機械設計に意味有るものとそうでない物がありますね。何の意味があるのか注釈を付けてくれるとやりがいが出てくると思うのですが。
高校の理科や社会では、副読本の資料集があるけど、数学にもあるといいね。数学事典の抜粋や数学史、各分野への応用など、いろいろ掲載して。https://twitter.com/genkuroki/status/848227993122095104 …
#数楽 同感です。教える側が数学を十分に勉強していれば面白くなる前の段階で切ってしまっている教科書の計算には対処できますが、そういう先生に出会えない高校生は対処できない。面白い計算につまらない印象が追加されてしまっている現状。https://twitter.com/ufoprofessor/status/848384828206530560 …

#数楽 例えば高校数学教科書、実教出版『数学III』2014年1月25日発行には、添付画像のような計算が載っています。一瞬だけ「おっ!今の高校の教科書にはWallisの公式が載っているのか!」と誤解する人は結構いるはず(笑)。でも実際には三角函数の定積分しかやっていない。続くpic.twitter.com/MdxO12um9p
#数楽 続き。「(sin x)^nの定積分の計算→nが偶数と奇数の場合の比較と不等式による評価→Wallisの公式」は定番のネタなのですが、最初の段階しかやっていない。個人的には「Wallisの公式」の段階で終わるのもつまらないと思うのに!続く
#数楽 続き。Wallisの公式はp=1/2の二項分布で2n回中n回成功する確率が1/√(nπ)のように振る舞うという結果です。確率論への応用がある。高校数学でよくある格子状の道の最短経路に関する組み合わせ論とWallisの公式を合わせると所謂「逆正弦法則」が証明できます。続く
#数楽 続き。「(sin x)^nの定積分の計算→nが偶数と奇数の場合の比較と不等式による評価→Wallisの公式→格子状の道の最短経路の組み合わせ論→逆正弦法則」ここまで理解できれば三角関数のべきの定積分の話がどのような現実の話に繋がっていることが明瞭になる。続く
#数楽 続き。あとWallisの公式はガンマ函数とベータ函数の漸近挙動の特別な場合。統計がらみの数学を勉強するとき、ちょっとしたおもちゃで遊んでみるためには、ガンマ函数とベータ函数の知識は必須。高校数学IIIの教科書にはガンマ函数とベータ函数関係の積分計算がたくさん載っています。
#数楽 続き。逆正弦法則については次のまとめを参照。https://twitter.com/i/moments/847098146660368384 …内容的にはまさに高校レベル。最短経路の個数を数えるだけの問題。このまとめに刺激されて、高校生でも気楽に読める解説を書いてくれる人が出て来るとうれしいです。
#数楽 単純ランダムウォークの逆正弦法則の証明のポイントは、正方形の角から反対側の角まで行く最短経路の個数binom(2n,n)=(2n)!/(n!)^2が直角三角形の45°の角から反対側の辺まで行く最短経路の個数に一致していることを示すことです。初等的かつ直観的な証明がある。

#数楽 個人的に実教出版『数学III』2014年1月25日発行の後半部分は結構好きです。同教科書から別の例を添付画像に引用しておきます。問題6は正規分布の問題。問題7はζ(2)の問題です。私にはそのような意図で教科書の執筆者達がこの問題を載せていることは明らかだと思う。pic.twitter.com/UN6RX47Rcx

#数楽 添付画像の問題の「もとネタ」もしくは「関連の数学の応用例」は「スターリングの近似公式」や「エントロピー」です。大雑把に言えば、「エントロピー=場合の数の対数」「相対エントロピー=確率の対数」です。場合の数や確率の計算には階乗が頻出なので階乗の対数の評価が重要になります。pic.twitter.com/QmN7sAEJHJ
#数楽 続き。一つ前のツイートの問題を「単に問題が解ければよい」という発想で扱う人はおそらくlog a_nの極限を区分求積法で処理してそれで終わりになってしまうと思う。それだと受験勉強適応的な取り扱いにしかならず、「まったくつまらない話であった」となっても仕方がないと思う。続く
#数楽 続き。数学の問題を解くことは数学の世界の様子を知るための手段に過ぎず、様子がよくわかっている数学の世界の範囲が広がれば入試問題を解くことなどくだらない問題に過ぎないということになってしまうはずなのに、低レベルな受験勉強適応的な学習で終わっている人が多いのではないか?
#数楽 続き。以上で引用した高校の数学の教科書にある問題を見れば「教科書の編集執筆者達は面白い話に繋がる問題を選んで載せる努力をしている」「しかしよい教師に出会わなければそのことが一般の高校生には伝わらないだろう」ということがわかると思います。色々もったいない話。
#数楽 階乗の簡単な評価(スターリングの公式)とその応用については以下のリンク先の解説(PDF)を見て下さい。http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf …http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf …
#数楽 スターリングの公式はn! = n^n e^{-n} √(2π) (1+O(1/n))もしくはlog n! = n log n - n + log√(2π) + O(1/n)です。これは数学の応用場面では空気のごとくよく使われます。
#数楽 訂正。√(2π)と書いていた部分を√(2πn)に訂正します。√nが足りなかった。https://twitter.com/genkuroki/status/848429626502168576 …

#数楽 あと、何度も言って来たことですが、高校数学IIIの教科書には昔から曲線の長さを積分で表せることが載っています。しかし、その取り扱いはとても小さくて、ラジアンの意味での角度がどのようにそれによって正当化されるかさえ何も書かれていない。pic.twitter.com/cQd0TuYD5r
#数楽 ググると「高校数学における三角関数の取り扱いは循環論法になっている」という有害な都市伝説の存在に気付きます。大学の数学の先生の一部がその都市伝説の源泉になっている疑いもあり、非常に嘆かわしいことだと思っています。続く
#数楽 続き。「曲線の長さは折れ線近似で定義しなければいけない」と誤解していたり、「三角関数を厳密に定義するためにはべき級数で定義するのがよい」という発想にとらわれている人が検索すると結構容易に見つかる。どうしてこんなことになっているのか。とても残念なことです。
#数楽 続き。y=sin θをθ=∫_0^y dt/√(1-t^2)の逆函数として定義する、θが単位円の弧の長さであることから、θがラジアンの意味での角度を意味することがわかり、その方針でのsin θの定義は高校数学でのsin θの定義に一致していることがわかります。続く
#数楽 続き。θ(y)=∫_0^y dt/√(1-t^2)が単位円の弧の長さであることは、x(t)=√(1-t^2)、y(t)=tに曲線の長さの積分表示を適用すればすぐにわかります。θ'(y)=1/√(1-y^2)から逆函数の導関数として(sin θ)'=cos θがすぐに出る。
#数楽 続き。要するに、lim_{θ→0}((sin x)/x)=1を示すことに三角関数の導関数の計算を帰着する方針はものすごく遠回りしているわけです。「単位円上の点のy座標を弧長の長さの函数とみなしたもの」というsin θの定義から直接出る計算を小難しくやっているだけ。続く
#数楽 続き。応用と無関係に「どのような定式化にすれば理論全体がすっきりきれいにまとまるか」という視点も数学ではとても重要です。思考の節約をするために定式化を工夫するという発想の気持ち良さを納得できる例として、単位円の弧長の積分表示から出発する三角関数論の展開は重要だと思う。
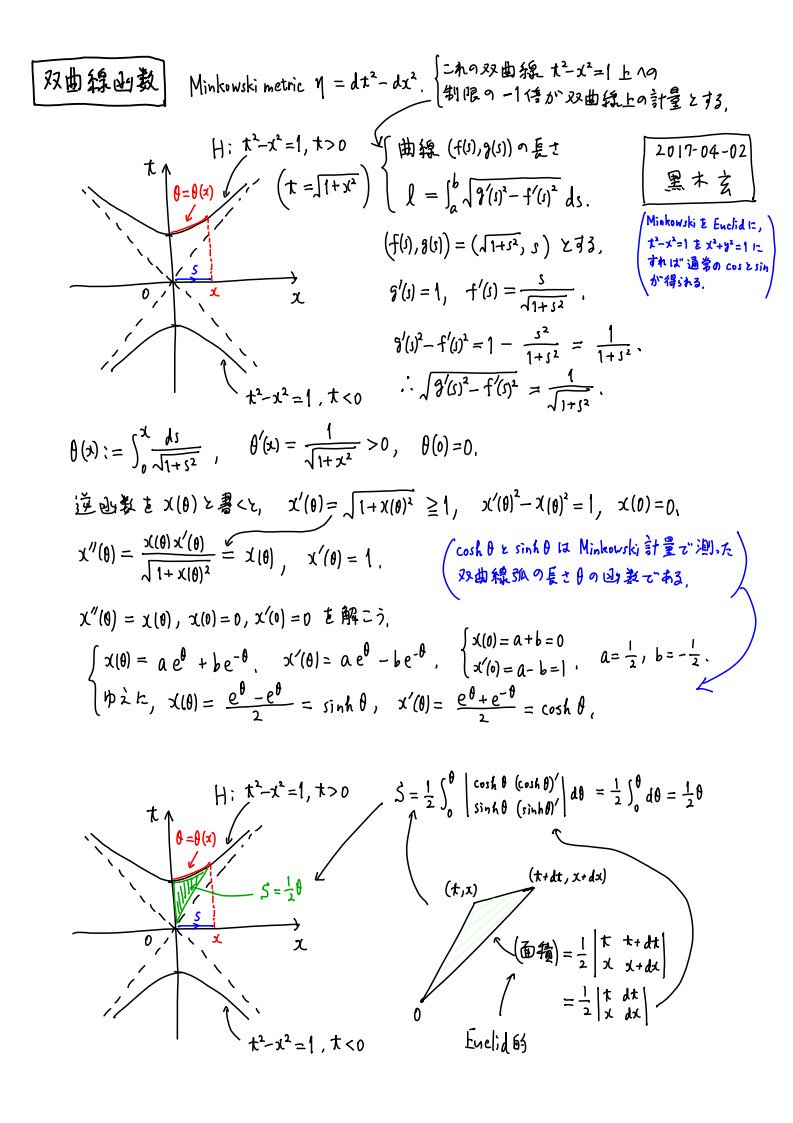
#数楽 sinh θのような双曲線函数は、三角函数論において長さをユークリッド的に測っていた部分をミンコフスキー計量に置き換えるだけで、得られます。双曲線函数におけるθはミンコフスキー計量で測った双曲線上の弧長の長さになっています。ユークリッドとミンコフスキーの違い。pic.twitter.com/g4fVDWh3my
#数楽 三角函数論も双曲線函数論も「不定積分で定義された函数の逆函数で函数を定義すると有用な函数が得られる」という普遍的なパターンの特別な場合。楕円函数論は被積分函数を1/√(3次または4次函数)とすれば同じ方針で得られます。ただし本質を理解するためには複素函数論が必須になる。
#数楽 双曲線函数論は双曲幾何版のトレミー(プトレマイオス)の定理を理解するために必須の道具になります。λ距離がe^θの形をしていることはcosh θ+sinh θ=e^θの一般化とみなせます。 θが測地線の長さでcosh θとsinh θの和はミンコフスキー内積。

#数楽 高校数学IIIの教科書が手元にある人は実際にガンマ函数やベータ函数に関係した積分があちこちに出て来ることを確認できる。添付画像はガンマ函数についてpic.twitter.com/TpDF8mZltK

#数楽 高校数学IIIの教科書には無限区間の積分は出て来ないんです。もったいない。数学を応用する場面では有限を無限で近似して取り扱いを易しくするというようなことがよく行われます。数学の応用の基本は理想化。だから無限区間の積分を使えないことは数学の応用的にはものすごいデメリット。
#数楽 返答連鎖の上の方の巨大添付画像を2枚読むだけで、∫_{-∞}^∞ e^{-y^2}dy=√(2π) (ガウス積分)、n!~n^n e^{-n} √(2πn) (スターリングの公式)の導出の仕方を学べる。
#数楽 極限の交換をおおらかにすることにすれば簡単。私は積極的におおらかであるべきだと思う。気になる人はおおらかにしてよいことを当然と思えるレベルの十分な論理的スキルを身に付けることが望ましい。おおらかでなくなる方向に進むのはとてもまずい。
#数楽 部分積分の応用で ∫ e^x sin ax dx を計算するというような話も高校数学IIIの教科書に載っていますが、その計算は三角函数のラプラス変換の計算と本質的に同じです。無限区間の積分を高校では扱わないのでラプラス変換やフーリエ変換はナマでは出て来ない。
#数楽 心ある人達は高校数学での積分の導入が「不定積分」「原始函数」からであることに不満を持っていると思います。しかし、定積分中心に改定するときには無限区間の積分も扱うようにしないと、現在の教科書で不定積分の形式で扱っている重要な計算のテクニックが削られてしまう危険性があります。
#数楽 「高校数学」のような分野を社会的に作ってしまったこと自体が数学教育的には失敗だったのではないか?数学は数学であり、「高校数学」や「基礎数学」の類は社会的に作られたものに過ぎず、そういう枠にとらわれた途端に肝腎の数学の理解は蔑ろにされてしまうと思う。
#数楽 質問:ベータ函数に関するB(s,1-s)=π/sin(πs)と∫_0^∞ du/(1+u^{1/s})=πs/sin(πs)は同値なのですが、これらを簡単に示す方法はないですかね?複素解析やガンマ函数の無限積表示などを使わない簡単な方法があれば教えて欲しいです。
#数楽 ちなみにWolframAlphaさんに不定積分 ∫du/(1+u^{1/s}) について効くと超幾何函数での表示を教えてくれます。http://www.wolframalpha.com/input/?i=\int+du/(1+u**{1/s} …)+
#数楽 B(p,q)=∫_0^∞ t^{p-1}dt/(1+t)^{p+q}なのですが、被積分函数の不定積分についてWolframAlphaさんに尋ねるとやはり超幾何函数表示を教えてくれます。http://www.wolframalpha.com/input/?i=\int+t^{p-1}dt/(1+t)^{p+q} …
本質的にガンマ函数に関するオイラーの反射公式を複素解析や無限積表示なしで微積分+αで証明せよという話ならデデキントの証明があります http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002148021 …Andrews-Askey-Royの49頁、問16参照。常微分方程式を解くところが難しいかも。

#数楽 https://twitter.com/Paul_Painleve/status/848536699743240192 …我々は文献にすぐにアクセスできるのですが(数学の本をたくさん保有している)、そうでない人たちが大部分だと思うので関連部分を抜き出して紹介しておきます。その1pic.twitter.com/rpPsn6LXRe

どうもありがとうございます。デデキントさんはこういう計算もしていたんですね。
#数楽 微分方程式 φφ''-(φ')^2=φ^4の解き方φ=1/fとおくと、その方程式はW(f,f')=ff''-(f')^2=-1に変換される。ゆえに(f,f')のWronskian W(f,f')が定数になるfを理解すればよい。続く
#数楽 一般にhがfとgの一次結合のときW(f,g,h)=0 (WはWronskian)。g=f'、W(f,f')=ff''-(f')^2=α=const.のとき、ff'''-f'f''=0となるので、W(f,g,h)=αh''+W(f',f'')hとなる。続く
#数楽 続き。h=fのときαf''+W(f',f'')f=0となり、両辺を微分して、αf'''+W(f',f'')f'+W(f',f'')'f=0.h=f'のときαf'''+W(f',f'')f'=0.それらの差を取ってW(f',f'')'f=0なのでW(f',f'')'=0.
#数楽 続き。W(f',f'')は定数。W(f',f'')=βとおくと、αf''+βf=0となり、fは定数係数の線形常微分方程式を満たすことがわかった。これを使えばff''-(f')^2=-1も解ける。もっと簡略化できそうだけど、深夜なのでやめておく。

#数楽 この手のことをやると複素解析を使った計算がどれだけ楽であるかがよくわかるよな。添付画像はいつもの解説ノート http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf … より。pic.twitter.com/Ow3etsmUos
#数楽 以上は以下のシンプルな定積分の話∫_0^∞ (t^{s-1}/(1+t))dt = π/sin πs∫_0^∞ (1/(1+u^{1/s})) du = πs/sin πs
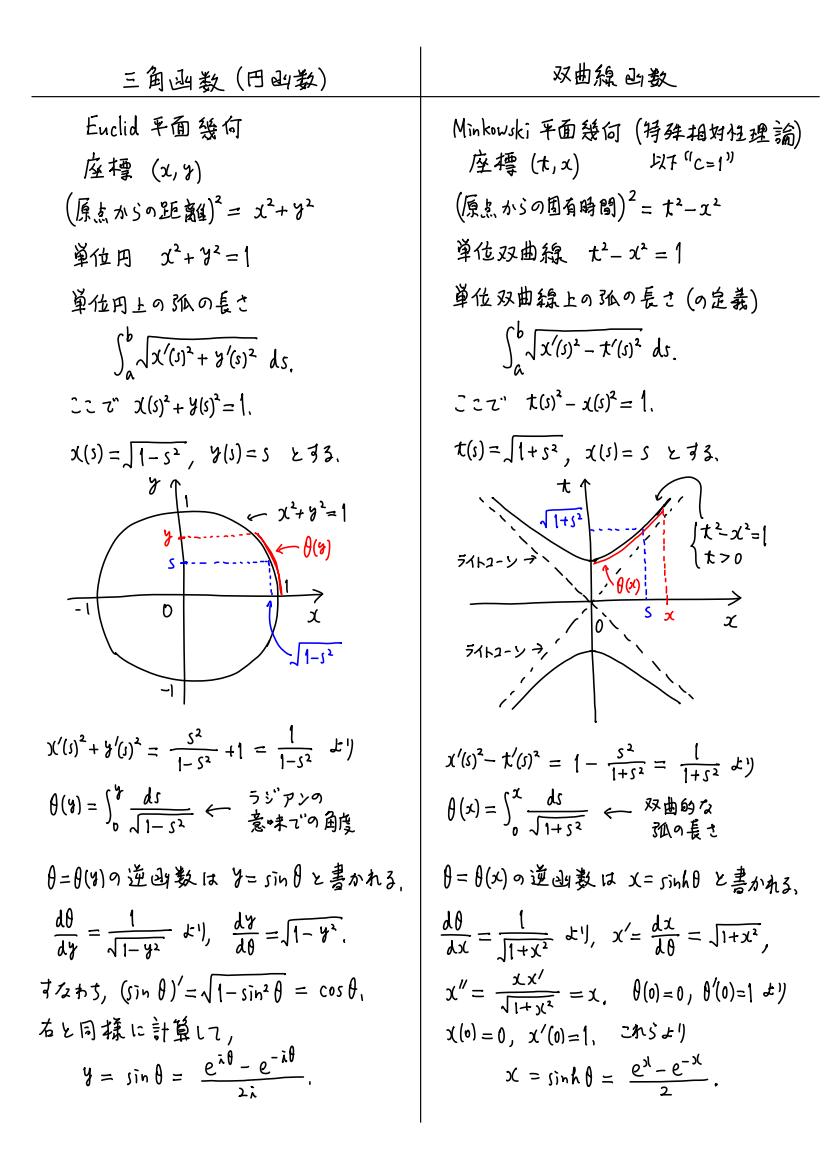
#数楽 https://twitter.com/genkuroki/status/848444518030430209 … に情報追加。三角函数(円函数)と双曲線函数の比較。この手のノートを自分で作りまくるのが数学の勉強の一つのスタイル。計算用紙を大量に消費することになる。pic.twitter.com/bZzE8jE9Ku
このノートはiPad Proでとっていらっしゃいますか?
それはiPadPro+Apple pencil+MetaMoji Noteで描きました。Windows+N-trig+Journalを使うこともあります。タブレット端末で描くときには投げ縄ツールがとても便利です。紙にできない道具を多用したいときにはタブレット端末で描きます。
#数楽 高校の数学の教科書の積分の計算の見せた方が「つまらないという印象を与える」感じになっているのではないか、と描きましたが、大学での微積分の教科書もそういう感じの教科書が多いと思う。これを言うと「おまえが教科書を書け」と言われそうなのでこずるく触れないでいた。
#数楽 昔からの定番の安全牌は高木貞治『解析概論』や寺沢寛一『自然科学者のための数学概論』だと思うのですが、教科書としては採用しにくい。高木貞治の概論概論は面白い計算がストーリーの中にたくさん挿入されており、証明をとばして計算を追うだけでも相当に勉強になると思います。
#数楽 私による解説http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …は高木貞治『解説概論』や寺寛と内容的に被らない話を書いたつもり。
#数楽 大学新入生が高木貞治『解析概論』を最初から読もうとすると最初の第1章の実数論で躓く可能性が高い。私が大学1年のときに聴いた黒田正先生の講義では、実数論やコンパクト性の結果を認めて先に進み、後で証明するという方針で、非常に易しく(優しく)聴きやすかったです。伝説の講義かも。
#数楽 高木貞治『解析概論』は真に面白い本なので、第1章で躓いて放り出す人が減って欲しいという願いがあるので、このような返答連鎖が出来上がる。返答連鎖を追えば私自身が『解析概論』を本当に楽しんでいることがわかると思います。日本語でこういう本があるのは歴史的に大変な幸運。
#数楽 ごめんなさい。高木貞治『解析概論』て楽しんだ件の返答連鎖はここではなくて、次のリンク先です。https://twitter.com/genkuroki/status/830016144933167104 …
#数楽 私は大学新入生のときに数学科の学生として伝説と言ってよいようなとても素晴らしい微積分の講義を聴くことができたのですが、そのときに高木貞治『解析概論』や佐武一郎『線型代数学』などを読むとよいと言われたのですが、それも幸運でした。そのアドバイスは現在も通用すると思う。
#数楽 「おまえが受けたような素晴らしい微積分の講義をおまえもやれ」と言われても残念ながら無理。私が受けた講義は1年かけて1変数の微積分しかやらなかった。内容的には非常に易しい講義。だから実数論+ε-δで押し通しても破綻しなかった。
#数楽 いずれにせよ、数学の勉強は「習うより慣れろ」にならざるを得ないので、どんな素晴らしい本を読んだり、講義を聴いても、慣れるまで(何らかの方法で)繰り返し試行錯誤した人以外は結果的に何も心に残さずに終わってしまうと思う。
#数楽 リンク先に補足。証明を読む前に例を計算して感触をつかもうとすることは定跡化された数学文献の読み方。計算してみてどこが面白いのか納得できてしまえば、結果的に証明も読めてしまうことが多い。https://twitter.com/genkuroki/status/849128862101364737 …
#数楽 現在 http://math.tohoku.ac.jp/~kuroki/LaTeX/ にアクセスできなくなっています。最近ずっと使いまわしている解説のコピーを以下の場所に置いておきました。http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …
#数楽 https://twitter.com/genkuroki/status/830016144933167104 …さらに、インターネット時代の現代では http://www.wolframalpha.com/ で気軽に数式処理ソフトを電卓のように利用できるし、こういうコアなネタに反応してくれる人と気軽にやりとりをできる。
#数楽 続き。計算がたくさん書いてある昔からある定番の本は E.T.Whittaker and G.N.Watson "A Course of Modern Analysis" https://www.google.co.jp/search?q=E.T.Whittaker+and+G.N.Watson+"A+Course+of+Modern+Analysis" … です。誰の計算かについてこの本にも書いてあります。
#数楽 まとめのリンク集をいきなり作るのは無理なので、こういう雑談の中でネタを増やして行くとよいと思う。誰かが話題にすればインターネット上に記録が残ってGoogle検索によって別の誰かが利用できるようになる。
三角函数と双曲線函数の微積分の基礎付けについては次のリンク先を見て下さい。「径路の長さが速さの積分で書けること」と「逆函数の導函数」からsinの微分がcosになることがすぐに出ます。面積経由は無用なステップを増やしているだけ。https://twitter.com/genkuroki/status/848918996275548160 …
角度は単位円弧の長さ∫_0^y ds/√(1-s^2)で定義され、扇型の面積は∫_0^y √(1-s^2) ds-y√(1-y^2)/2になるのですが、扇型の面積を角度で表すためには前者で後者を表すことになります。単に余計な手間が増えるだけです。
リンク先は双曲線函数に関する解説ですが、三角函数も同様であり、返答連鎖の前後に色々書いてあります。https://mobile.twitter.com/genkuroki/status/848444518030430209 …
#数楽 高校レベルの積分の計算問題関係の話がリンク先のモーメントにまとまっています。最近の高校の数学の教科書の様子も少し紹介してあります。https://twitter.com/i/moments/848450692645662720 …



